3.2 Práctica Guiada

library(fs)
library(tidyverse)
library(openxlsx)
library(glue)

3.2.1 Ejemplo 1: Iterando en la EPH

Lo primero que necesitamos es definir un vector o lista sobre el que iterar.

Por ejemplo, podemos armar un vector con los path a las bases individuales, con el comando fs::dir_ls

bases_individuales_path <- dir_ls(path = 'fuentes/', regexp= 'individual')
bases_individuales_path

## fuentes/usu_individual_t119.txt fuentes/usu_individual_t418.txt

Luego, como en la función que usamos para leer las bases definimos muchos parametros, nos podemos armar una función wrapper que sólo necesite un parámetro, y que simplifique la escritura del map

leer_base_eph <- function(path) {
  read.table(path,sep=";", dec=",", header = TRUE, fill = TRUE) %>% 
    select(ANO4,TRIMESTRE,REGION,P21,CH04, CH06)
}

bases_df <- tibble(bases_individuales_path) %>%
  mutate(base = map(bases_individuales_path, leer_base_eph))

bases_df

## # A tibble: 2 x 2
##   bases_individuales_path         base                 
##   <fs::path>                      <list>               
## 1 fuentes/usu_individual_t119.txt <df[,6] [59,369 × 6]>
## 2 fuentes/usu_individual_t418.txt <df[,6] [57,418 × 6]>

El resultado es un DF donde la columna base tiene en cada fila, otro DF con la base de la EPH de ese período. Esto es lo que llamamos un nested DF o dataframe nesteado pa les pibes.

Si queremos juntar todo, podemos usar unnest()

bases_df <- bases_df %>% unnest()
bases_df

## # A tibble: 116,787 x 7
##    bases_individuales_path          ANO4 TRIMESTRE REGION   P21  CH04  CH06
##    <fs::path>                      <int>     <int>  <int> <int> <int> <int>
##  1 fuentes/usu_individual_t119.txt  2019         1     41     0     2    28
##  2 fuentes/usu_individual_t119.txt  2019         1     41     0     2    13
##  3 fuentes/usu_individual_t119.txt  2019         1     41     0     1     1
##  4 fuentes/usu_individual_t119.txt  2019         1     41  5000     2    41
##  5 fuentes/usu_individual_t119.txt  2019         1     41     0     2     9
##  6 fuentes/usu_individual_t119.txt  2019         1     41  8000     1    51
##  7 fuentes/usu_individual_t119.txt  2019         1     41     0     1    63
##  8 fuentes/usu_individual_t119.txt  2019         1     41     0     2    62
##  9 fuentes/usu_individual_t119.txt  2019         1     41     0     2    24
## 10 fuentes/usu_individual_t119.txt  2019         1     41  3000     1    74
## # … with 116,777 more rows

¿Qué pasa si los DF que tenemos nesteados no tienen la misma cantidad de columnas?

Esto mismo lo podemos usar para fragmentar el datastet por alguna variable, con el group_by()

bases_df %>% 
  group_by(REGION) %>% 
  nest()

## # A tibble: 6 x 2
## # Groups:   REGION [6]
##   REGION           data
##    <int> <list<df[,6]>>
## 1     41   [11,509 × 6]
## 2     44   [14,204 × 6]
## 3     42   [11,150 × 6]
## 4     43   [34,702 × 6]
## 5     40   [24,432 × 6]
## 6      1   [20,790 × 6]

Así, para cada región tenemos un DF.

¿ De qué sirve todo esto?

No todo en la vida es un Dataframe. Hay estucturas de datos que no se pueden normalizar a filas y columnas. En esos casos recurríamos tradicionalmente a los loops. Con MAP podemos tener los elementos agrupados en un sólo objeto y aún conservar sus formas diferentes.

3.2.2 Ejemplo 2. Regresión lineal

Si bien no nos vamos a meter en el detalle del modelo lineal hoy, es útil usarlo como ejemplo de lo que podemos hacer con MAP.

Planteamos el modelo \[ P21 = \beta_0 + \beta_1*CH04 + \beta_2*CH06 \] Osea, un modleo que explica el ingreso según sexo y edad

lmfit <- lm(P21~factor(CH04)+CH06,data = bases_df)

summary(lmfit)

## 
## Call:
## lm(formula = P21 ~ factor(CH04) + CH06, data = bases_df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -15472  -6606  -3367   2148 590198 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    4853.196     74.509   65.14   <2e-16 ***
## factor(CH04)2 -4063.112     72.200  -56.27   <2e-16 ***
## CH06            103.095      1.612   63.97   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 12300 on 116784 degrees of freedom
## Multiple R-squared:  0.05511,    Adjusted R-squared:  0.0551 
## F-statistic:  3406 on 2 and 116784 DF,  p-value: < 2.2e-16

(al final de la clase podemos charlar sobre los resultados, si hay interés :-) )

De forma Tidy, la librería broom nos da los resultados en un DF.

broom::tidy(lmfit)

## # A tibble: 3 x 5
##   term          estimate std.error statistic p.value
##   <chr>            <dbl>     <dbl>     <dbl>   <dbl>
## 1 (Intercept)      4853.     74.5       65.1       0
## 2 factor(CH04)2   -4063.     72.2      -56.3       0
## 3 CH06              103.      1.61      64.0       0

Si lo queremos hacer por region

3.2.2.1 Loopeando

resultados <- tibble()

for (region in unique(bases_df$REGION)) {
  
  data <- bases_df %>% 
    filter(REGION==region)
  
  lmfit <- lm(P21~factor(CH04)+CH06,data = data)
  
  lmtidy <- broom::tidy(lmfit)
  lmtidy$region <- region
  resultados <- bind_rows(resultados,lmtidy)

}

resultados

## # A tibble: 18 x 6
##    term          estimate std.error statistic   p.value region
##    <chr>            <dbl>     <dbl>     <dbl>     <dbl>  <int>
##  1 (Intercept)     3768.     185.        20.3 3.15e- 90     41
##  2 factor(CH04)2  -3814.     180.       -21.2 6.00e- 98     41
##  3 CH06             106.       4.18      25.3 1.12e-137     41
##  4 (Intercept)     7156.     291.        24.6 1.09e-130     44
##  5 factor(CH04)2  -5938.     278.       -21.4 1.42e- 99     44
##  6 CH06             145.       6.32      23.0 1.40e-114     44
##  7 (Intercept)     4930.     231.        21.4 2.15e- 99     42
##  8 factor(CH04)2  -4007.     224.       -17.9 1.71e- 70     42
##  9 CH06              97.8      4.95      19.7 2.68e- 85     42
## 10 (Intercept)     5107.     131.        39.0 0.            43
## 11 factor(CH04)2  -3949.     127.       -31.1 5.02e-209     43
## 12 CH06              83.5      2.78      30.0 3.87e-195     43
## 13 (Intercept)     3329.     128.        26.0 4.12e-147     40
## 14 factor(CH04)2  -3239.     125.       -25.9 3.74e-146     40
## 15 CH06             122.       2.89      42.2 0.            40
## 16 (Intercept)     5196.     197.        26.4 3.45e-151      1
## 17 factor(CH04)2  -4051.     189.       -21.4 1.80e-100      1
## 18 CH06              88.2      4.12      21.4 1.98e-100      1

3.2.2.2 Usando MAP

Primero me armo una funcion que me simplifica el codigo

fun<-function(porcion,...) {  broom::tidy(lm(P21~factor(CH04)+CH06,data = porcion))}

bases_df_lm <- bases_df %>%
  group_by(REGION) %>%
  nest() %>%
  mutate(lm = map(data,fun))
bases_df_lm

## # A tibble: 6 x 3
## # Groups:   REGION [6]
##   REGION           data lm              
##    <int> <list<df[,6]>> <list>          
## 1     41   [11,509 × 6] <tibble [3 × 5]>
## 2     44   [14,204 × 6] <tibble [3 × 5]>
## 3     42   [11,150 × 6] <tibble [3 × 5]>
## 4     43   [34,702 × 6] <tibble [3 × 5]>
## 5     40   [24,432 × 6] <tibble [3 × 5]>
## 6      1   [20,790 × 6] <tibble [3 × 5]>

bases_df_lm %>%
  unnest(lm)

## # A tibble: 18 x 7
## # Groups:   REGION [6]
##    REGION           data term        estimate std.error statistic   p.value
##     <int> <list<df[,6]>> <chr>          <dbl>     <dbl>     <dbl>     <dbl>
##  1     41   [11,509 × 6] (Intercept)   3768.     185.        20.3 3.15e- 90
##  2     41   [11,509 × 6] factor(CH0…  -3814.     180.       -21.2 6.00e- 98
##  3     41   [11,509 × 6] CH06           106.       4.18      25.3 1.12e-137
##  4     44   [14,204 × 6] (Intercept)   7156.     291.        24.6 1.09e-130
##  5     44   [14,204 × 6] factor(CH0…  -5938.     278.       -21.4 1.42e- 99
##  6     44   [14,204 × 6] CH06           145.       6.32      23.0 1.40e-114
##  7     42   [11,150 × 6] (Intercept)   4930.     231.        21.4 2.15e- 99
##  8     42   [11,150 × 6] factor(CH0…  -4007.     224.       -17.9 1.71e- 70
##  9     42   [11,150 × 6] CH06            97.8      4.95      19.7 2.68e- 85
## 10     43   [34,702 × 6] (Intercept)   5107.     131.        39.0 0.       
## 11     43   [34,702 × 6] factor(CH0…  -3949.     127.       -31.1 5.02e-209
## 12     43   [34,702 × 6] CH06            83.5      2.78      30.0 3.87e-195
## 13     40   [24,432 × 6] (Intercept)   3329.     128.        26.0 4.12e-147
## 14     40   [24,432 × 6] factor(CH0…  -3239.     125.       -25.9 3.74e-146
## 15     40   [24,432 × 6] CH06           122.       2.89      42.2 0.       
## 16      1   [20,790 × 6] (Intercept)   5196.     197.        26.4 3.45e-151
## 17      1   [20,790 × 6] factor(CH0…  -4051.     189.       -21.4 1.80e-100
## 18      1   [20,790 × 6] CH06            88.2      4.12      21.4 1.98e-100

O incluso más facil, utilizando group_modify (que es un atajo que solo acepta DF)

bases_df %>% 
  group_by(REGION) %>% 
  group_modify(fun)

## # A tibble: 18 x 6
## # Groups:   REGION [6]
##    REGION term          estimate std.error statistic   p.value
##     <int> <chr>            <dbl>     <dbl>     <dbl>     <dbl>
##  1      1 (Intercept)     5196.     197.        26.4 3.45e-151
##  2      1 factor(CH04)2  -4051.     189.       -21.4 1.80e-100
##  3      1 CH06              88.2      4.12      21.4 1.98e-100
##  4     40 (Intercept)     3329.     128.        26.0 4.12e-147
##  5     40 factor(CH04)2  -3239.     125.       -25.9 3.74e-146
##  6     40 CH06             122.       2.89      42.2 0.       
##  7     41 (Intercept)     3768.     185.        20.3 3.15e- 90
##  8     41 factor(CH04)2  -3814.     180.       -21.2 6.00e- 98
##  9     41 CH06             106.       4.18      25.3 1.12e-137
## 10     42 (Intercept)     4930.     231.        21.4 2.15e- 99
## 11     42 factor(CH04)2  -4007.     224.       -17.9 1.71e- 70
## 12     42 CH06              97.8      4.95      19.7 2.68e- 85
## 13     43 (Intercept)     5107.     131.        39.0 0.       
## 14     43 factor(CH04)2  -3949.     127.       -31.1 5.02e-209
## 15     43 CH06              83.5      2.78      30.0 3.87e-195
## 16     44 (Intercept)     7156.     291.        24.6 1.09e-130
## 17     44 factor(CH04)2  -5938.     278.       -21.4 1.42e- 99
## 18     44 CH06             145.       6.32      23.0 1.40e-114

Pero MAP sirve para operar con cualquier objeto de R.

Por ejemplo podemos guardar el objeto S3:lm que es la regresion lineal entrenada. Ese objeto no es ni un vector, ni una lista, ni un DF. No es una estructura de datos, sino que es algo distinto, con propiedades como predict() para predecir, el summary() que vimos, etc.

fun<-function(porcion,grupo) {  lm(P21~factor(CH04)+CH06,data = porcion)}

bases_df %>% 
  group_by(REGION) %>%
  nest() %>%  
  mutate(lm = map(data,fun))

## # A tibble: 6 x 3
## # Groups:   REGION [6]
##   REGION           data lm    
##    <int> <list<df[,6]>> <list>
## 1     41   [11,509 × 6] <lm>  
## 2     44   [14,204 × 6] <lm>  
## 3     42   [11,150 × 6] <lm>  
## 4     43   [34,702 × 6] <lm>  
## 5     40   [24,432 × 6] <lm>  
## 6      1   [20,790 × 6] <lm>

3.2.3 Ejemplo 3: Gráficos en serie

Veamos un tercer ejemplo con otra base de datos que ya conocemos: Gapminder, que muestra algunos datos sobre la población de los países por año.

El objetivo de este ejercicio es hacer un gráfico por país de forma automática.

Primero veamos los datos

library(gapminder)


gapminder_unfiltered %>% 
  sample_n(10)

## # A tibble: 10 x 6
##    country       continent  year lifeExp       pop gdpPercap
##    <fct>         <fct>     <int>   <dbl>     <int>     <dbl>
##  1 Italy         Europe     2002    80.2  57926999    27968.
##  2 Sierra Leone  Africa     2007    42.6   6144562      863.
##  3 United States Americas   1959    70.0 177830000    15240.
##  4 Lithuania     FSU        2000    72.1   3654387     9632.
##  5 Bulgaria      Europe     1993    71.2   8441872     6367.
##  6 Norway        Europe     1953    73.2   3360888    10393.
##  7 Australia     Oceania    2007    81.2  20434176    34435.
##  8 New Zealand   Oceania    1950    69.3   1908310    11449.
##  9 Mongolia      Asia       1972    53.8   1320500     1422.
## 10 France        Europe     1953    67.3  42751746     7171.

la base tiene la siguiente info:

country: Nombre del país
continent: Nombre del continente
year: año
lifeExp: Esperanza de vida al nacer
pop: Población
gdpPercap
Vamos a hacer un gráfico sencillo para Argentina

data_argentina <- gapminder_unfiltered %>% 
  filter(country=='Argentina')

ggplot(data_argentina, aes(year, lifeExp, size= pop, color=gdpPercap))+
  geom_point()+
  geom_line(alpha=0.6)+
  labs(title = unique(data_argentina$country))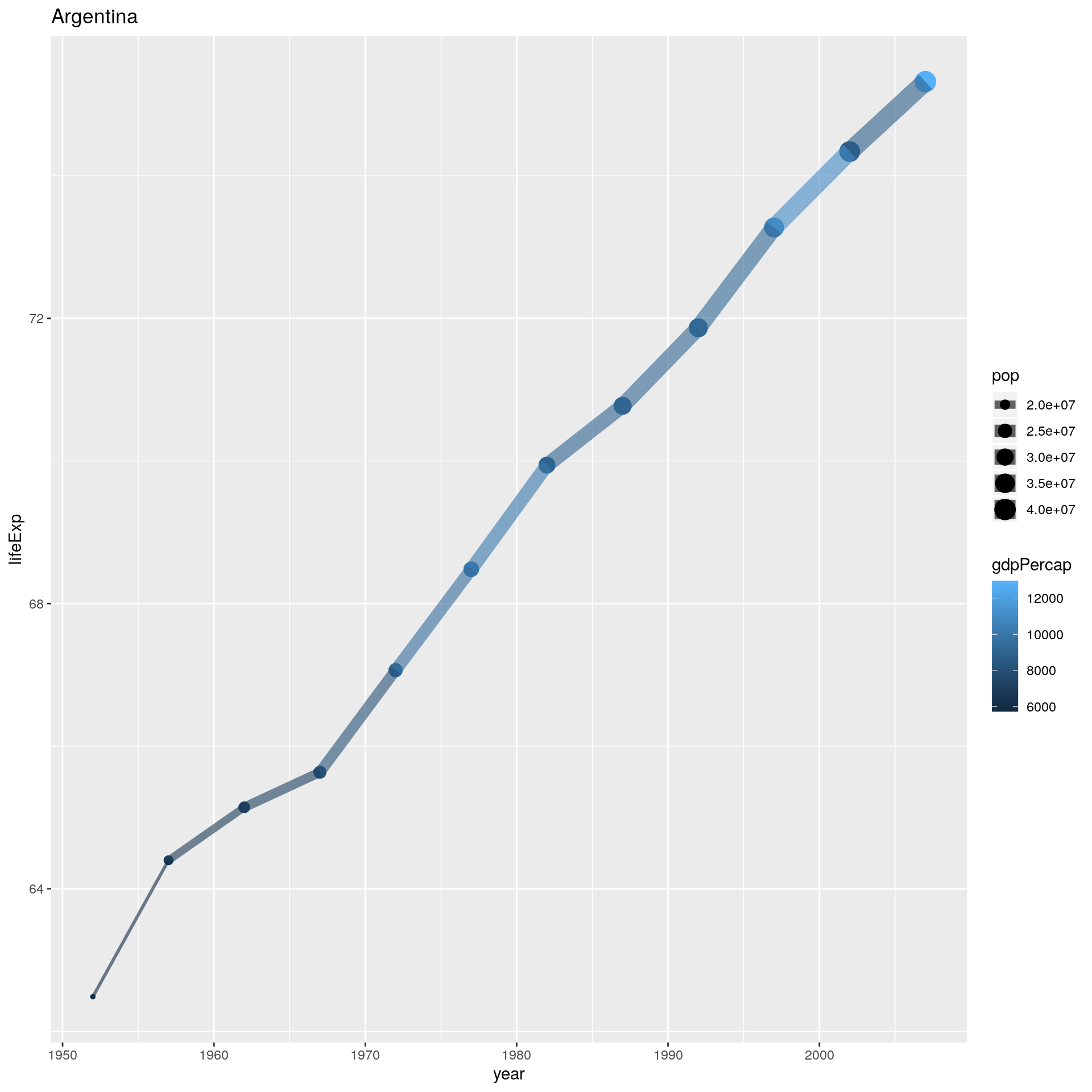

Ahora que tenemos una idea de lo que queremos gráficar lo podemos poner adentro de una función que grafique.

# definimos la función
graficar_pais <- function(data, pais){
  
  ggplot(data, aes(year, lifeExp, size= pop, color=gdpPercap))+
    geom_point()+
    geom_line(alpha=0.6)+
    labs(title = pais)
}

probamos la función para un caso

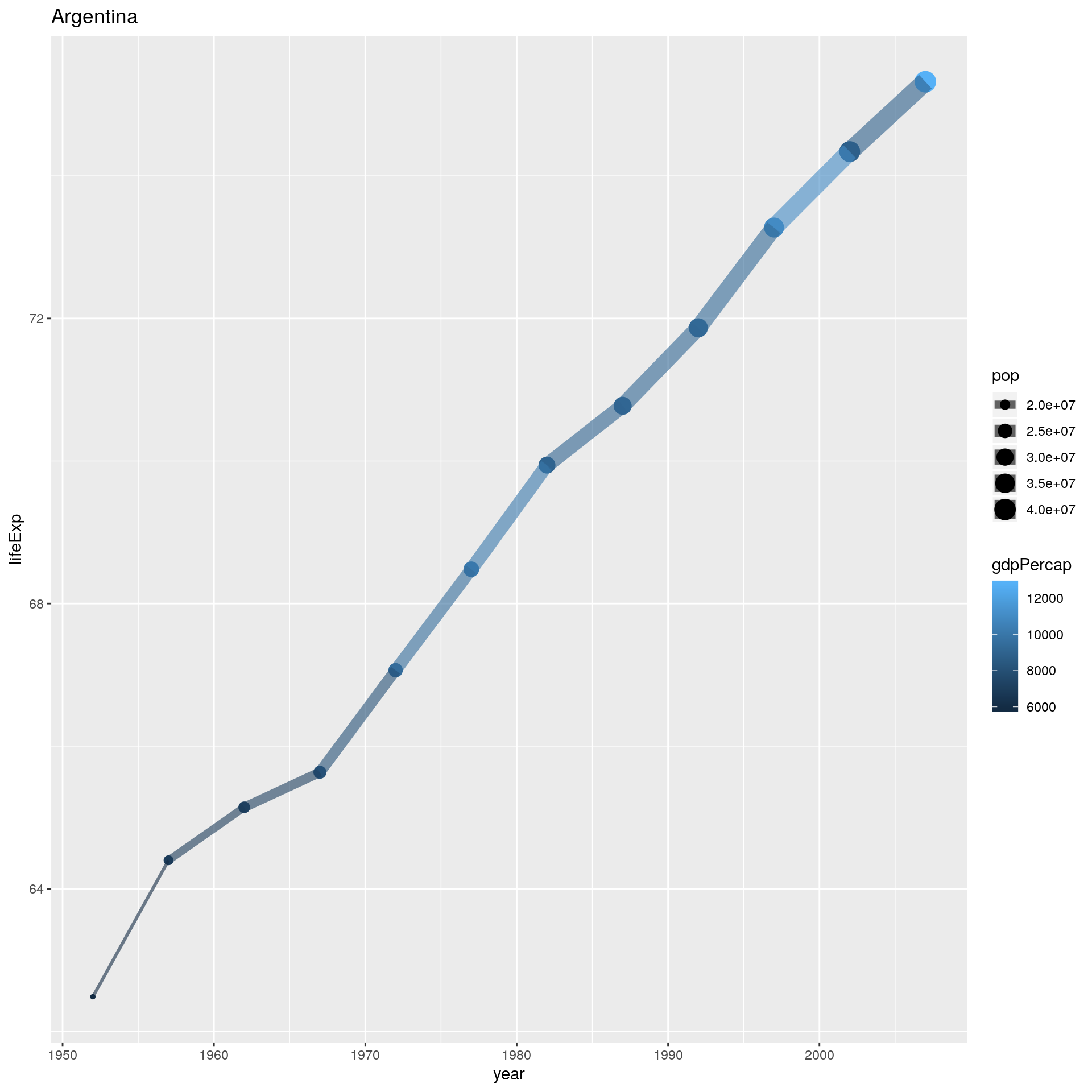
graficar_pais(data_argentina, 'Argentina')

Nos armamos un dataset nesteado

gapminder_nest <- gapminder_unfiltered %>% 
  group_by(country) %>% 
  nest()

gapminder_nest[1:10,]

## # A tibble: 10 x 2
## # Groups:   country [187]
##    country               data
##    <fct>       <list<df[,5]>>
##  1 Afghanistan       [12 × 5]
##  2 Albania           [12 × 5]
##  3 Algeria           [12 × 5]
##  4 Angola            [12 × 5]
##  5 Argentina         [12 × 5]
##  6 Armenia            [4 × 5]
##  7 Aruba              [8 × 5]
##  8 Australia         [56 × 5]
##  9 Austria           [57 × 5]
## 10 Azerbaijan         [4 × 5]

Ahora podemos crear una nueva columna que contenga los gráficos

gapminder_nest <- gapminder_nest %>% 
  mutate(grafico= map2(.x = data, .y = country,.f =  graficar_pais))

gapminder_nest[1:10,]

## # A tibble: 10 x 3
## # Groups:   country [187]
##    country               data grafico
##    <fct>       <list<df[,5]>> <list> 
##  1 Afghanistan       [12 × 5] <gg>   
##  2 Albania           [12 × 5] <gg>   
##  3 Algeria           [12 × 5] <gg>   
##  4 Angola            [12 × 5] <gg>   
##  5 Argentina         [12 × 5] <gg>   
##  6 Armenia            [4 × 5] <gg>   
##  7 Aruba              [8 × 5] <gg>   
##  8 Australia         [56 × 5] <gg>   
##  9 Austria           [57 × 5] <gg>   
## 10 Azerbaijan         [4 × 5] <gg>

Veamos un ejemplo

gapminder_nest$grafico[2]

## [[1]]

Ahora podemos guardar todos los gráficos en un archivo PDF

pdf('resultados/graficos_gapminder.pdf')
gapminder_nest$grafico
dev.off()