7.2 Práctica Guiada

library(tidyverse)

7.2.1 Generación de datos aleatorios

Para generar datos aleatorios, usamos las funciones:

• rnorm para generar datos que surgen de una distribución normal
• rt para generar datos que surgen de una distribución T-student
• rchisq para generar datos que surgen de una distribución Chi cuadrado
• runif para generar datos que surgen de una distribución uniforme > Pero antes, tenemos que fijar la semilla para que los datos sean reproducibles

set.seed(1234)
rnorm(n = 15,mean = 0, sd = 1 )

##  [1] -1.20706575  0.27742924  1.08444118 -2.34569770  0.42912469
##  [6]  0.50605589 -0.57473996 -0.54663186 -0.56445200 -0.89003783
## [11] -0.47719270 -0.99838644 -0.77625389  0.06445882  0.95949406

rt(n = 15,df=1 )

##  [1] -0.363717710 -1.603466805 -0.388596796 -0.588007490  0.007839245
##  [6] 14.690527710 -1.863488555  0.022667470 -2.084247299 -0.249237745
## [11] -1.311594174 -3.569055208 -2.490838240 -3.848779244 -4.271087169

rchisq(n = 15,df=1)

##  [1] 0.5317744 1.4263809 4.2797098 0.2184660 0.6923773 0.0455256 3.1902100
##  [8] 0.2949942 0.5403827 0.1543732 0.8639196 0.1417290 1.1386091 0.2966193
## [15] 0.5110879

runif(15,0,1)

##  [1] 0.75911999 0.42403021 0.56088725 0.11613577 0.30302180 0.47880269
##  [7] 0.34483055 0.60071414 0.07608332 0.95599261 0.02220682 0.84171063
## [13] 0.63244245 0.31009417 0.74256937

hagamos un ggplot para visualizar la info

tibble(normal = rnorm(n = 15,mean = 0, sd = 1 ),
       tstudent = rt(n = 15,df=1 ),
       chi = rchisq(n = 15,df=1),
       uniforme = runif(15,0,1)) %>%
  gather(distribucion,valor) %>% 
  ggplot(aes(distribucion,valor,fill=distribucion))+
  geom_violin()+
  facet_wrap(.~distribucion,scales = 'free')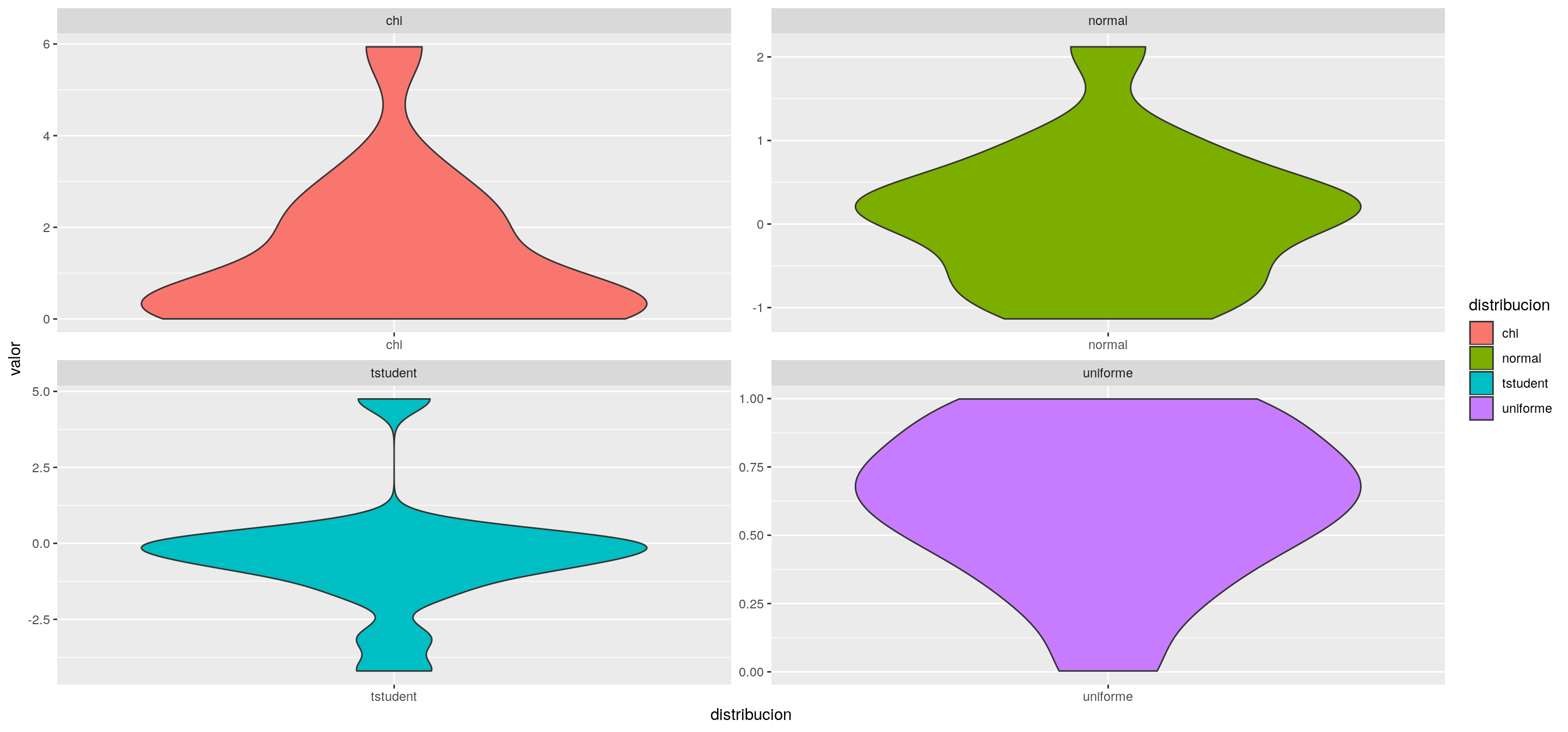

Qué pasa si lo corremos varias veces?

7.2.2 Tests

dist1 <- rnorm(100, 10,sd = 1)
dist2 <- rnorm(100, 15, sd = 1)


t.test(dist1,dist2, paired = F,var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  dist1 and dist2
## t = -33.391, df = 198, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -5.059234 -4.494982
## sample estimates:
## mean of x mean of y 
##  10.17864  14.95575

dist1 <- rnorm(10, 10,sd = 1)
dist2 <- rnorm(10, 15, sd = 1)


t.test(dist1,dist2, paired = F,var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  dist1 and dist2
## t = -8.9832, df = 18, p-value = 4.529e-08
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -5.963134 -3.702580
## sample estimates:
## mean of x mean of y 
##  10.05722  14.89008

dist1 <- rnorm(5, 10,sd = 1)
dist2 <- rnorm(5, 15, sd = 1)


t.test(dist1,dist2, paired = F,var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  dist1 and dist2
## t = -6.8836, df = 8, p-value = 0.0001266
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -5.335167 -2.657580
## sample estimates:
## mean of x mean of y 
##  10.07898  14.07535

dist1 <- rnorm(20, 10,sd = 2)
dist2 <- rnorm(20, 11, sd = 1)


t.test(dist1,dist2, paired = F,var.equal = F)

## 
##  Welch Two Sample t-test
## 
## data:  dist1 and dist2
## t = -3.618, df = 29.93, p-value = 0.00108
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.5848637 -0.7194778
## sample estimates:
## mean of x mean of y 
##   9.68726  11.33943

7.2.3 Descripción estadística de los datos

Volvamos a ver los datos de sueldos de funcionarios

sueldos <- read_csv('fuentes/sueldo_funcionarios_2019.csv')

Con el comando summary podemos ver algunos de los principales estadísticos de resumen

summary(sueldos$asignacion_por_cargo_i)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  197746  210061  226866  225401  231168  249662

7.2.4 Gráficos estadísticos

A modo de ejemplo, dejamos los comandos de R base para realizar gráficos.

mamiferos <- openintro::mammals

ggplot(mamiferos, aes(y=LifeSpan))+
  geom_boxplot()

ggplot(mamiferos, aes(BodyWt, BrainWt,label=Species))+
  geom_point()

ggplot(mamiferos, aes(log(BodyWt), log(BrainWt),label=Species))+
  geom_point()